1. 그래프란 무엇인가?
그래프(Graph)란 노드(정점, Vertex)들의 집합이며,
이 노드들은 간선(Edge)을 통해 서로 연결되어 있다.
그래프는 트리(Tree) 자료구조와 유사하지만, 연결 방식에서 차이가 있는데,
예를 들어, N개의 노드를 가진 트리는 항상 N-1개의 간선을 가지며, 각 간선은 부모-자식 관계를 형성한다.
트리에서는 모든 노드가 루트 노드로부터 단 하나의 경로로 연결될 수 있다.
반면, 그래프에서는 노드 간에 정해진 관계(부모-자식)가 없으며, 이로 인해 노드들이 다양한 방식으로 자유롭게 연결될 수 있다.
간선은 2가지 타입으로 나뉘는데,
- Directed edges는 연결이 한 방향(단방향)인 간선을 의미
이때 한쪽 끝점은 출발지, 다른 한쪽 끝점은 도착지 - Undirected edges는 연결이 양방향(양방향)인 간선을 의미
즉, 두 정점이 서로 자유롭게 오갈 수 있다.
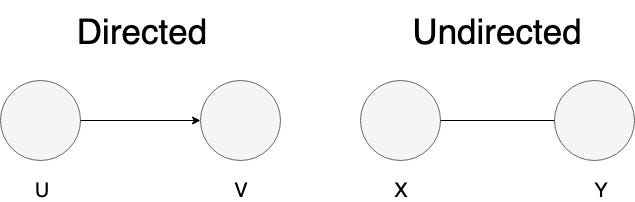
Directed Edge는 순서쌍으로 표현될 수 있다. 위 사진의 U, V는 (U, V)로 표현된다
단방향 표현식이기 때문에 U -> V는 가능하지만, V -> U는 불가능하다
Undirected Edge는 <U, V>로 표현될 수 있으며, 일반적으로는 모든 간선이 방향이 있거나(directed) or 방향이 없는(undirected) 한 종류로만 구성되지만, 두 방식이 혼합된 그래프도 존재할 수 있다

Q. 그래프는 어디에 사용될까?
소셜 네트워크(Twitter, Instagram)의 경우 방향 그래프(Directed Graph)로 표현이 가능하다
누군가를 팔로우할 수는 있지만, 그 사람이 나를 다시 팔로우 하는 것은 아니기에 상대방이 팔로우를 눌렀을 때 비로소 양방향 연결이 된다
2. 그래프 가중치
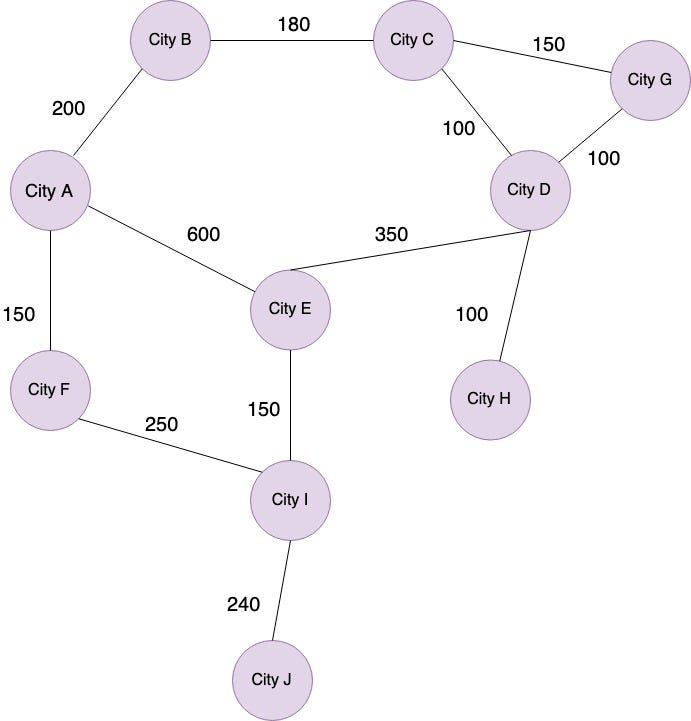
그래프의 간선에는 가중치(Weight)를 부여할 수 있다.
가중치는 보통 거리, 비용, 시간 등 특정한 "비용"을 의미하며, 이를 통해 그래프를 더 현실적으로 표현할 수 있다.
예를 들어, 도시 A에서 도시 D로 가는 최소 거리를 탐색한다고 했을 때,
- 경로 1: A → E → D (노드를 적게 거침)
- 경로 2: A → B → C → D (노드를 더 많이 거침)
표면적으로는 첫 번째 경로가 더 빠를 것 처럼 보이지만, 실제로는 다를 수 있다.
- A → E → D의 총 거리가 1.05km
- A → B → C → D의 총 거리가 0.48km
위와 같이, 노드를 더 많이 거치더라도 두 번째 경로가 효율적인 선택이 된다
이처럼, 그래프에 가중치를 두어 현실 상황을 정밀하게 표현할 수 있다
3. 그래프의 표현법 2가지
I. 인접 행렬이란?
인접 행렬은 그래프의 연결관계를 이차원 배열로 나타내는 방식이다
인접 행렬이 adj[i][j]로 정의되어 있다면, 표현은 다음과 같다
adj[i][j] = 1 : i -> j로 향하는 간선이 존재한다
adj[i][j] = 0 : i -> j로 향하는 간선이 존재하지 않는다
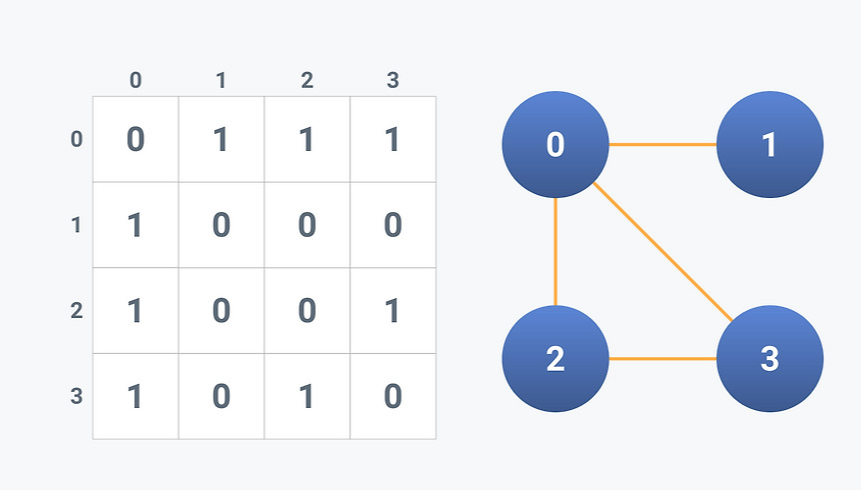
II. 장점 및 단점
<장점>
- 구현이 쉽다
- 요소 접근 시, O(1)
<단점>
- 연결된 노드에 방문하고 싶은 경우, 모든 노드를 확인해보아야하기 때문에 adj[i][0]부터 adj[i][N]까지 탐색하는 경우 O(N)의 시간이 걸린다
III. 인접 리스트란?
그래프에서 각 노드가 간선을 리스트로 표현한 방식
adj = [0, 1, 2, 3]이라는 리스트가 존재할 때, 다음과 같이 표현할 수 있다
adj = {
0: [1, 2, 3],
1: [0],
2: [0, 3],
3: [0, 2]
}
각 표현의 의미는 다음과 같다
adj[0][1] = 3 // 0 -> 1로 향할 때, 가중치 3
adj[0][2] = 5 // 0 -> 2로 향할 때, 가중치 5

IV. 장점 및 단점
<장점>
- 실제로 연결된 노드에 대해만 저장 => 간선 개수에 비례하는 메모리만 차지, 메모리 효율 ⬆️
- 실제로 연결된 노드만 확인 => 요소 탐색 시, 시간 감소
<단점>
- 반면, 요소 접근 시 O(N)의 시간 복잡도
4. 그래프의 활용(DFS, BFS)
I. 깊이 우선 탐색(DFS, Depth First Search)
다음 요소를 탐색하기 전에, 현재 탐색 중인 노드를 깊게 탐색하는 방법
루트 노드에서 시작하여, 해당 분기를 완벽하게 탐색하는 방식을 지칭

위 사진과 같이 탐색이 시작되면 현재 노드의 최대 깊이까지 탐색을 진행한다. 탐색이 끝나야 비로소 다음 노드 탐색을 시작한다
II. 너비 우선 탐색(BFS, Breadth-First Search)
가장 인접한 노드들을 먼저 탐색하여, 최대한 넓게 이동하며 탐색하는 방법

'CS > 개념' 카테고리의 다른 글
| 위상 정렬(topological sort) 개념 및 구현하기 (0) | 2025.06.03 |
|---|---|
| [CSAPP Chapter3 3.1 ~ 3.4]프로그램의 기계수준 표현 (0) | 2025.05.31 |
| [자료구조] 트리(tress) 정의 및 구현하기 (0) | 2025.05.30 |
| 해시테이블(Hash Table)이란? (0) | 2025.05.26 |
| 우선순위 큐와 힙 이해하기 (0) | 2025.05.26 |