1. 부동 소수점 정의
부동 소수점(floating point)이란?
부동(浮動) : 뜰 부(浮)에 움직일 동(動) => 떠서 움직인다
즉, 소수점의 위치가 정해지지 않은 소수를 '부동 소수점'이라고 합니다.
컴퓨터가 메모리를 효율적으로 사용하면서, 더 많은 수를 표현하기 위한 방식입니다
2. 고정 소수점 vs 부동 소수점
고정 소수점과 부동 소수점은 어떤 차이가 있을까요?
우선, 고정 소수점은 소수점을 기준으로 정수부와 소수부로 나뉩니다

이는 저희가 수학 시간에 배웠던 기본적인 실수 표현 방식이죠
부동소수점은 이와 다르게 가수과 지수로 수를 표현합니다

대략적으로 설명하자면, 가수는 수를 나타내는 영역이고, 지수는 수가 얼마나 큰지를 나타냅니다
예를 들어, 위 사진에서 12.345 x 10^1을 1.2345 x 10^2라고 표현할 수도 있겠죠?
이처럼 가수는 고정되어 어떤 수인지 표현하며, 지수는 소수점을 이동하면서 수가 얼마나 크거나 작은지 나타냅니다
아직 가수와 지수의 개념, 부동 소수점이 무엇인지 헷갈릴 것 같습니다.
두 개념을 더 자세히 알아보기 위해서 -12.375라는 고정소수점을 부동소수점으로 표현해보도록 하겠습니다
3. 고정 소수점 → 부동소수점 변환 과정 살펴보기
목표 : -12.375을 32비트 부동소수점으로 표현하기
고정 소수점을 부동 소수점으로 변환하기에 앞서, 컴퓨터가 어떻게 부동소수점을 저장하는지 알아보겠습니다
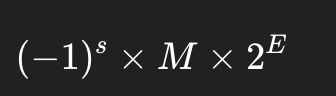
위는 부동 소수점을 나타내는 표현식이며, 아래는 컴퓨터가 부동소수점을 저장하는 방식을 나타냅니다.
S(sign, 부호비트) = 0이면 양수, 1이면 음수
M(Mantissa, 가수) = 숫자의 값 표현
E(Exponent, 지수) = 숫자가 얼마나 큰지 작은지 표현
-12.375가 정규화 과정을 거쳐, 부동 소수점으로 변환되면 다음과 같이 변환됩니다
1.100011 * 2^3
(가수) = 100011 (공백인 값들은 모두 0으로 채움)
= 10001100000000000000
(지수) 3 => 2진수 변환 0100
그러나, 아래 사진 지수 부분을 보면 알 수 있듯이, 0100이 아닌 1000010이라는 이상한 값이 들어갔습니다.
이는 127+3 = 130을 2진수 변환하여 넣은 값인데요
왜 127이라는 값을 더해서 지수 부분을 표현했는지는 아래에서 자세히 살펴보겠습니다
여태까지 부동소수점이
1) 어떻게 표현되는지
2) 컴퓨터가 부동 소수점을 어떻게 저장하는지 알아보았으니, 다음으로 고정 소수점을 부동 소수점으로 변환하는 과정을 따라가보겠습니다

1단계: 부호(Sign)
-12.375 : 음수
Sign : 1
---
2단계 : 10진수 → 2진수 변환
정수부 : 12
- 12 = 1100 (2진수)
소수부 : 375
- 0.375 * 2 = 0.75 → 정수 0
- 0.75 * 2 = 1.5 → 정수 1
- 0.5 * 2 = 1.0 → 정수 1
0.375 = 0.011 (2진수)
최종 : 12.735 => 1100.011 (10진수 -> 2진수)
---
3단계: 정규화 된 값
1.100011 * 2^3
---
4단계: 지수 계산(Exponent)
실제 지수 E = 3
bias = 127
지정할 지수 = E + bias = 130
130 = 10000010
* 정규화와 지수 계산은 아래에서 자세히 설명하겠습니다
---
5단계 : 가수
1.100011 중 소수점 뒤만 저장 → 100011
나머지 비트는 0으로 채움
M(가수) = 10001100000000000000000
---
6단계 : 결과 (-12.375의 부동소수점 표현)
Sign + 지수 + 가수
1 10000010 10001100000000000000000
위 과정을 거쳐, 부동 소수점 1 10000010 10001100000000000000000을 저장할 수 있는 형태로 변환이 완료되었습니다
변환 과정에서 *정규화와 *bias라는 생소한 표현들이 있었는데, 이것들은 무엇을 의미할까요?
3-1 정규화
소수점을 옮겨서 항상 숫자를 1.xxx... × 2^e 형태로 만드는 것
즉, 12.735 => 1100.011 (10진수 -> 2진수)
위 2진수를 1.100011 x 2^3으로 표현하는 것을 '정규화'라고 합니다
정규화로 수를 표현하는 이유로는 1. 표현의 일관성 2. 수를 정밀하게 표현
위 2가지 이유가 있습니다
만약, 정규화 과정을 거치지 않는다면 12.735라는 수를 1100.011으로 표현할 수도, 1.100011 x 2^3으로도 표현할 수 있겠죠?
컴퓨터는 이 값들을 모두 다른 값으로 인식하기 때문에 정규화 과정을 거쳐, 부동 소수점 일관성 있게 표현합니다
또한, 최상위 비트(정수 부분)이 항상 1이기 때문에, 정수 부분이 아닌 소수 부분만 저장하여, 더 많은 수를 표현할 수 있게 됩니다
3-2 편향된 지수
부동소수점 표현에서 지수를 저장할 때는 “실제 지수”를 그대로 저장하지 않고,
“bias(편향값)”을 더한 값을 저장합니다. 이걸 편향된 지수 방식(Biased Exponent)이라고 합니다
---
Q. 왜 bias(편향값)을 사용할까?
지수(Exponent)는 양수일 수도, 음수일 수도 있습니다
예:
- 1.23 × 2³ → 지수 = 3 (양수)
- 4.56 × 2⁻² → 지수 = -2 (음수)
그런데 컴퓨터는 음수를 저장하기가 번거롭습니다.
→ 음수 표현엔 부호 비트(+, -)가 필요하고, 이로인해 회로가 복잡합니다
-> 지수가 항상 양수처럼 보이게 만들기 위해 127이라는 값을 미리 더해서 저장합니다.
이 값을 bias (편향값) 라고 부릅니다.
---
Q. 왜 편향값(bias)은 127인가?
이때까지의 설명은 모두 32비트 기준으로 설명드렸습니다
32비트 부동소수점에서는 지수부가 8비트이며,
8비트는 00000000부터 11111111까지, 즉 0부터 255까지 표현할 수 있죠
그 중 가운데 값인 127을 기준점(bias)로 삼으면 다음과 같이 표현이 가능합니다 :
- 실제 지수가 0일 때, 저장되는 값은 127
- 실제 지수가 +1일 때, 저장되는 값은 128
- 실제 지수가 -1일 때, 저장되는 값은 126
이렇게 하면 음수 지수를 양수처럼 보이는 숫자로 저장할 수 있어서 훨씬 간단해집니다.
---
3-3 편향된 지수 마무리
3. 고정 소수점 -> 부동 소수점 변환 과정에서 정규화된 값은 다음과 같았습니다:
- 실제 지수 E = 3
- bias = 127
- 저장할 지수 = E + bias = 130
- 130 = 10000010 (8비트)
실제 지수는 3이지만, 모든 수를 양수'처럼' 표현하기 위해 항상 bias값을 더하여 2진수 변환을 하는 것이죠
'CS > 개념' 카테고리의 다른 글
| 해시테이블(Hash Table)이란? (0) | 2025.05.26 |
|---|---|
| 우선순위 큐와 힙 이해하기 (0) | 2025.05.26 |
| 스택과 큐( + linked list queue) 알아보기 (0) | 2025.05.24 |
| 이진탐색(binary search)란 무엇인가? (python) (0) | 2025.05.23 |
| 병합 정렬(Merge sort)개념 및 구현 방법(python) (1) | 2025.05.22 |